
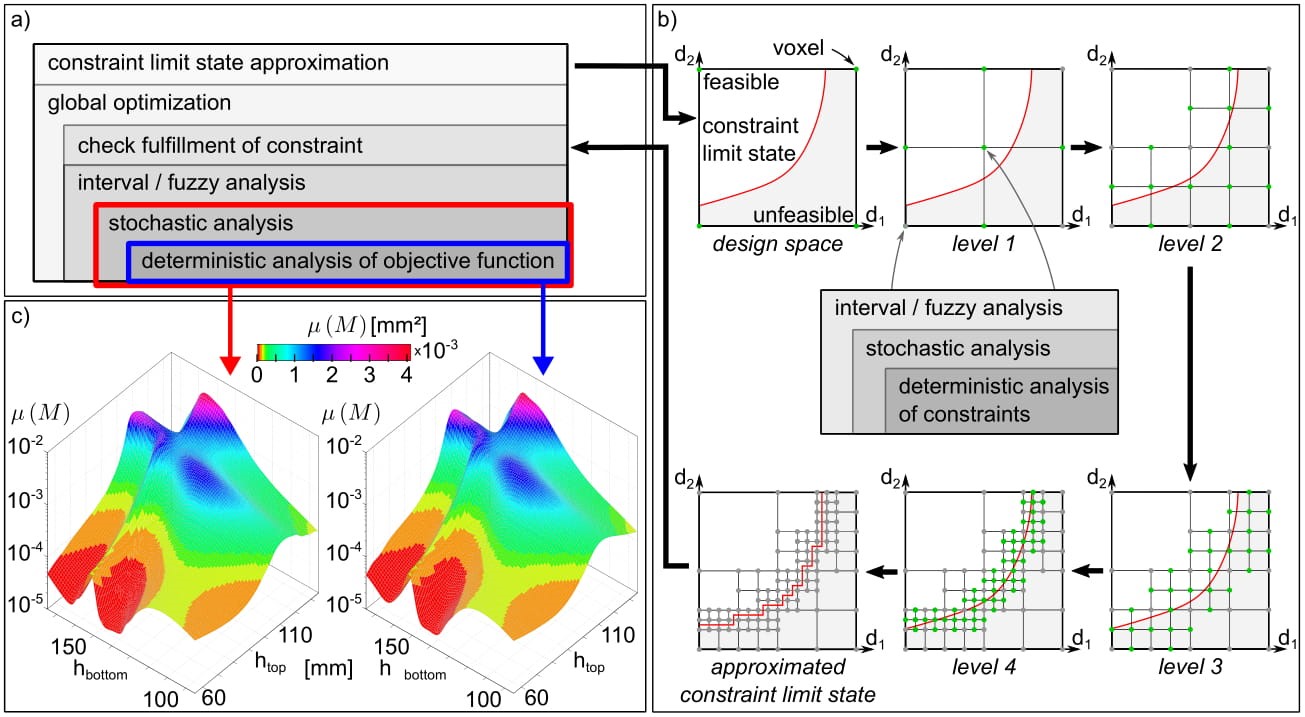
For the numerical design of reinforced concrete structures, a framework combining optimization algorithms with polymorphic uncertainty models has been developed, see Figure 1a and [1]. The particle swarm optimization algorithm in combination with stochastic and interval uncertainty models has been implemented and different objectives for uncertain quantities of interest have been formulated. To reduce the computation time of the optimization, a space subdividing technique (see Figure 1b) for the consideration of inequality constraints has been adopted in [2]. A surrogate modelling strategy has been developed to replace the nonlinear finite element simulations, where the deterministic simulation as well as the stochastic analysis are approximated by sequentially trained artificial neural networks, see Figure 1c. In [3], this approach has been extended to a multilevel surrogate modelling strategy, where also the interval analysis is approximated by a third artificial neural network.
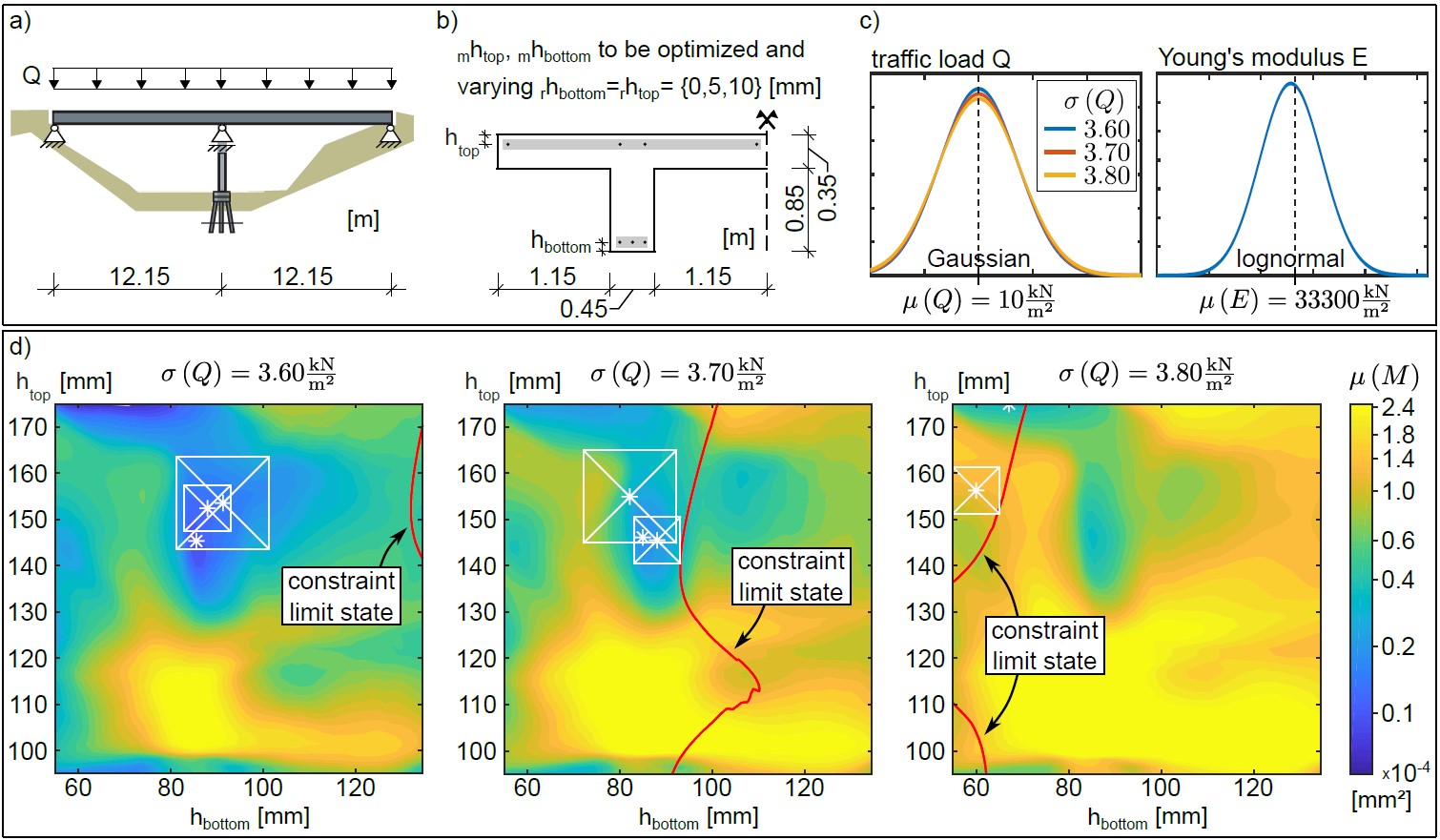
Exemplified, the concrete cover of the lower and upper reinforcement layer of a reinforced concrete bridge structure has been optimized by minimizing the exposed lateral surface of the reinforcement crossing a crack, see [2]. The design parameters have been modelled as intervals with different radii to account for construction imprecision, while the material parameters of concrete (Young’s modulus and fully correlated tension and compression strength) and the traffic load are modelled as a priori stochastic variables. As a constraint, the accepted failure probability with respect to the load bearing capacity has been defined. Nine combinations of rebar arrangements have been analysed in [1], followed by further investigations of the best rebar arrangement [2] with respect to the sensitivity of the interval radii and the standard deviation of the load. It was found, that the optimal value of the objective function is exponentially increasing with increasing interval radius. It was observed, that slight variations of the standard deviation of the traffic load lead to large changes of the constraint limit state and to variations of the objective function and the optimal designs, see Figure 2.
M.Sc. Philipp Edler
philipp.edler@rub.de
+49 234 / 32-29069

"Adaptive insertion of interface elements for fracture analysis: Reliable computation of interface t
more...
Chen Xu, Giao Vu, Ba Trung Cao, Zhen Liu, Fabian Diewald, Yong Yuan, and Günther Meschke are the au
more...