Concrete subjected to cyclic loading experiences progressive degradation which can reduce the load carrying capacity of structures and lead to premature damage and failure. In order to gain insights into the nature of the progressive damage in concrete, in the scope of the DFG Priority Program 2020, the influence of heterogeneity and disorder on the meso-scale level of concrete is currently being investigated numerically at the institute of Structural Mechanics.
Failure of concrete subjected to tension is not perfectly brittle, but shows a post-peak softening in the load displacement curve as observed routinely in experiments since the 1960s. This post-peak softening has been attributed to the existence of a non-negligible fracture process zone (FPZ) formed in regions of material that experience very high stress concentrations, (e.g. near the defects, notch tips, etc.) as a consequence of high heterogeneity of concrete. In this zone various fracture processes occur, such as diffuse damage in form of micro-cracking that develop ahead of the crack tip and shield the crack tip from stress concentrations or crack wake processes such as crack face bridging by unbroken aggregates and ligaments which resist crack face opening and thus provide residual stiffness in the post-peak regime. The processes described above are crucial for understanding of failure of concrete both under quasi-static and cyclic loading. In preliminary work two approaches are considered for analysis of the influence of material disorder on damage evolution in concrete under quasi-static uniaxial loading: 1) a fiber bundle model, and 2) a 2-dimensional high-fidelity finite element model based on element erosion.

The fiber bundle model
The fiber bundle is a simple model originating from theoretical physics used to model the failure of disordered materials. The fiber bundle consists of many parallel fibers, with varying elastic properties and strengths, clamped between two plates. The breaking of the fibers can be thought of as debonding process occurring in real materials during fracture. The strength thresholds of fibers in a bundle are sampled according to the Weibull distribution (Fig. 1).

As the load is increased, the fibers fail one by one as their strength thresholds are reached and after the peak load is reached, bundles with global load sharing mechanism exhibit softening behavior under a displacement controlled experiment (Fig. 2).

High fidelity erosion based Finite Element model The meso-structure of cement paste is modelled by means of high resolution finite element model based on element erosion in order to gain insight into the similarities of the failure mechanisms occurring in this setting with the 1D fiber bundle models. A notched square specimen is loaded in uniaxial tension. At the peak load, damage localizes into a single crack and the specimen ultimately fails (Fig. 3 and Fig. 4). The specimen experiences significant diffuse damage before the dominant crack starts propagating from the notch. Even after the localization of damage, diffuse damage occurs around the ’crack tip’ (Fig. 4).

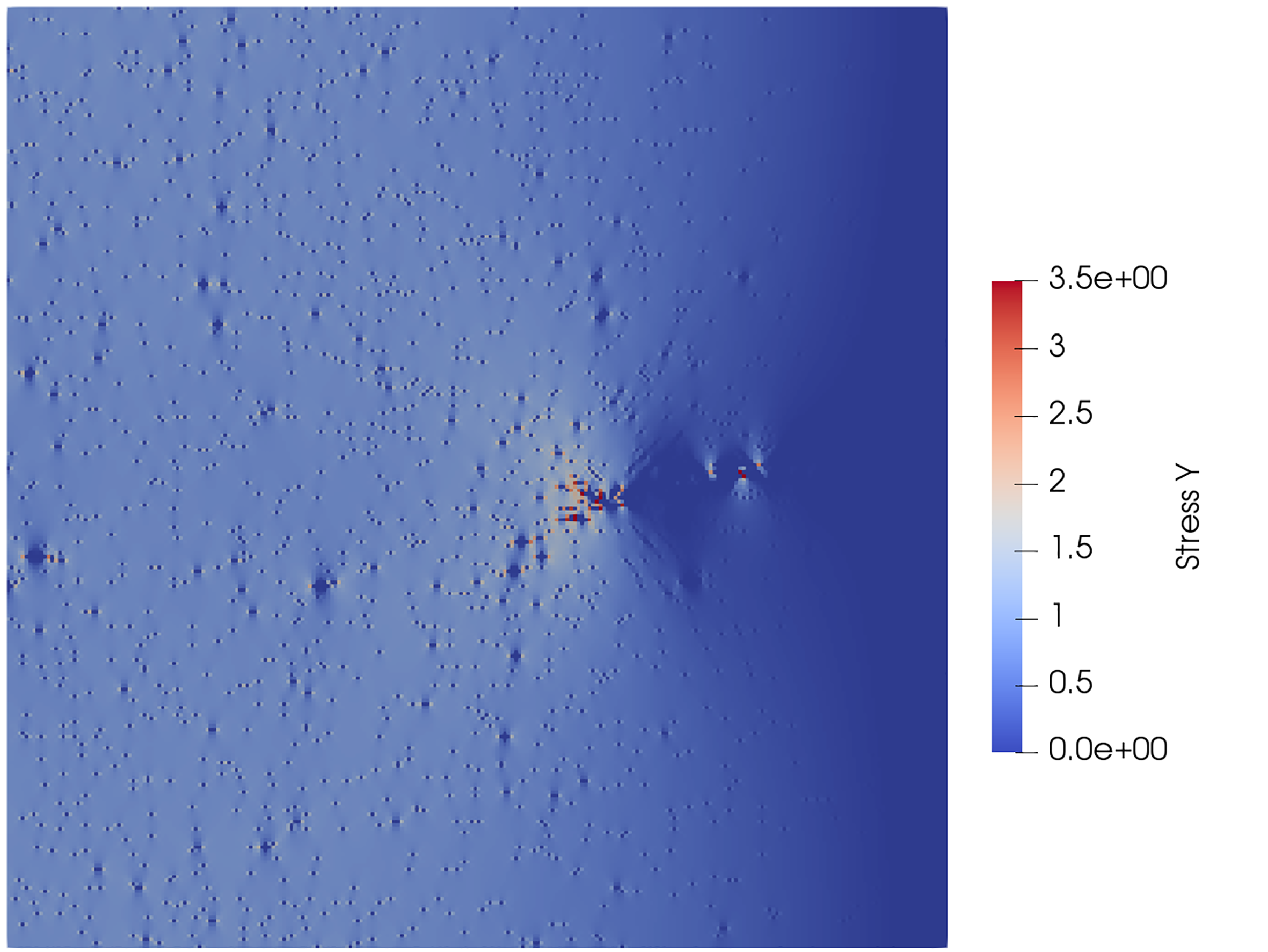
Furthermore, crack face bridging can be observed, indicated by stress concentration in the unbroken ligaments that bridge the crack. In order to gain more insight into the influence of strength randomness, a series of 500 stochastic numerical experiments have been conducted on the same specimen, with different realizations of the strength thresholds, sampled from Weibull distribution. The resulting load-displacement curves are presented in Figure 5 and they show, on average, some residual load-carrying capacity of the specimen in the post-peak regime.

The evolution of the progressive damage in disordered heterogeneous materials such as concrete is a highly complex three-dimensional problem. The extension of the described models to handle 3D dynamic load cases considering the detailed microstructure of concrete with and without micro-fiber reinforcement is currently under development at the institute of Structural Mechanics.

Contact

M.Sc. Vladislav Gudzulic
Vladislav.Gudzulic@ruhr-uni-bochum.de
+49 234 / 32-29072